CMSC 27100 — Lecture 10b: Graph Proofs and Isomorphisms

Now that we've gotten some definitions out of the way, we can talk about why we care about why graphs are a whole unit in this course. Of course graphs are an important structure in computer science, but it turns out that reasoning about them can be surprisingly tricky. This unit is intended to show you what the point of working through the previous two units was. Number theory and combinatorics may not come up directly in CS very often, but each of them taught us some very important lessons about writing proofs and solving problems that will help us with graphs.

Graphs, as in Unit 1, are well-defined items with rigorous definitions that need to be argued about. Writing proofs on graphs requires us to be logically consistent, to structure our argument well, and to sometimes be creative with how we manipulate the objects we are given to create new ones.

That said, more like Unit 2, graphs also have a lot of properties that can be argued about through analog or comparison. They definitely feel more tangible than the natural numbers themselves, and lend themselves to the ability to make arguments more like Unit 2 that rely to some extent on the intuition we have about what these objects are like.

The obvious thing to do here, of course, is to string together our two paths. In real life, if there's a path from $u$ to $v$ and a path from $v$ to $w$, then clearly if we want to go from $u$ to $w$ we'd just walk from $u$ to $v$ and from $v$ to $w$. However, remember that a path, as defined, can not repeat any vertices! Consider the following graph. Here, the first path goes from $u$ to $v$ and is highlighted in red. The second path from $v$ to $w$ is in blue. If one naively takes the union of the paths, then the result is not a path (for example, it has a cycle).

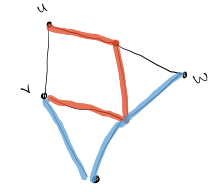
However, this picture also gives us a sense of how we might actually approach the problem. There's clearly a path from $u$ to $w$ in this graph that follows the red path until they intersect and follows the blue path to get to $w$. Let's look at a formal proof.

Let $a_0,\ldots,a_m$ be a path from $u=a_0$ to $v=a_m$ and $b_0,\ldots,b_n$ be a path from $v=b_0$ to $w=b_n$. Denote by $i$ the smallest value where $a_i = b_j$ for some $j$. Then consider the sequence \[u=a_0, a_1, ..., a_{i-1}, a_i=b_j, b_{j+1}, ..., b_{n-1}, b_n=w. \]

To show that this sequence is a path, we must argue that it is both a walk and does not repeat any vertices. It clearly is a walk - any two consecutive vertices here were consecutive vertices in a valid path, so they must have been adjacent.

Arguing that it does not repeat any vertices is a bit more tricky. Of course, none of the $a$ values can repeat because they are part of a path, and none of the $b$ values can repeat for the same reason, so the only possible repeats are the existence of some $i', j'$ on this walk where $a_{i'} = b_{j'}$ but $i \neq i'$ or $j \neq j'$. Assume for contradiction that they exist. Then because they are on this walk, we must have either $i' < i$, which contradicts the claim that $i$ is the smallest value we could have chosen, or $i'=i$, which means that $b_{j'} = a_{i'} = a_{i} = b_{j}$, so $j'=j$, contradiction. Thus, no repeated vertices can exist in this walk, so it is a path.

You can see here that our statement was incredibly straightforward and probably pretty intuitive, but still required us to do a good amount of analysis and careful considering to write our formal proof. This is where our learnings from Unit 1 are important - we need to make sure each step is logically sound and that our proof as a whole actually shows what we want it to.

Now let's look at another one. This one also follows intuition pretty naturally - if there's a way to walk between two points, then you can do so without repeating any points.

Consider the walk $u = v_0 v_1 \cdots v_k = v$ from $u$ to $v$ of minimum length $k$ (we are invoking the well-ordering principle here). If no vertex is repeated, then we can form a path from $u$ to $v$ in the obvious way. So suppose for contradiction that a vertex is repeated. In other words, there exist $i, j$ with $i \lt j$ such that $v_i = v_j$. Then we can create a shorter walk \[ u = v_0 v_1 \cdots v_{i-1} v_i v_{j+1} v_{j+2} \cdots v_k = v, \] which is valid since $v_iv_{j+1} = v_jv_{j+1}$. We have deleted $j-i\geq 1$ vertices, so this contradicts the minimality of the length of our original walk. Thus there are no repeated vertices in our walk and therefore we can form a path from $u$ to $v$.

Again, we're invoking some relatively heavy machinery for our proof compared to how obvious the statement appears to be. We could have tried to prove this a different way, perhaps by inducting on the number of repeated vertices in the walk, which is possible but would require us to be very careful with how this trimming process described in the proof interacts with different repeated vertices.

It turns out that this theorem, Theorem 10.15, is pretty powerful despite how obvious it seems. For example, it gives us a much shorter proof of Theorem 10.14 by saving the original attempt we made.

Let $a_0,\ldots,a_m$ be a walk from $u=a_0$ to $v=a_m$ and $b_0,\ldots,b_n$ be a walk from $v=b_0$ to $w=b_n$. Consider the sequence \[ a_0,\ldots,a_m,b_1,\ldots,b_n. \] Note that we've started from $b_1$. This is a valid walk because $a_m = v = b_0$. Moreover, it is a walk from $u$ to $w$. Theorem 10.15 implies there is a path from $u$ to $w$.

Another sort of "common sense" theorem says that if we have two distinct paths with the same ends, then we have a cycle in our graph. Be careful: distinct doesn't mean disjoint. In other words, the two paths can share some vertices and edges, but will contain different edges at some point.

Consider two distinct paths $P_1$ and $P_2$ between vertices $u$ and $v$. Let $a_0,a_1,\ldots,a_m$ be the vertices of $P_1$ and $b_0,b_1,\ldots,b_n$ be the vertices of $P_2$, where $a_0 = b_0 = u$ and $a_m=b_n=v$, but $m$ is not necessarily equal to $n$. Since the two paths are distinct, there is an edge that is in one path but not the other. Without loss of generality, suppose $a_ia_{i+1}$ is in $P_1$ but not $P_2$.

Consider the graph $G - a_ia_{i+1}$, that is, $G$ without the edge $a_ia_{i+1}$. Now, consider the walk \[ a_i a_{i-1} \cdots a_0 b_1 \cdots b_n a_{n-1} \cdots a_{i+1}. \] This walk is valid because $a_0 = b_0$ and $b_n = a_n$, and it is from $a_i$ to $a_{i+1}$. Moreover, it does not use the edge $a_ia_{i+1}$. By the previous theorem, there is a path between $a_i$ and $a_{i+1}$ in $G - a_ia_{i+1}$. Then the addition of the edge $a_ia_{i+1}$ to this path forms a cycle in $G$.

Graph Isomorphisms

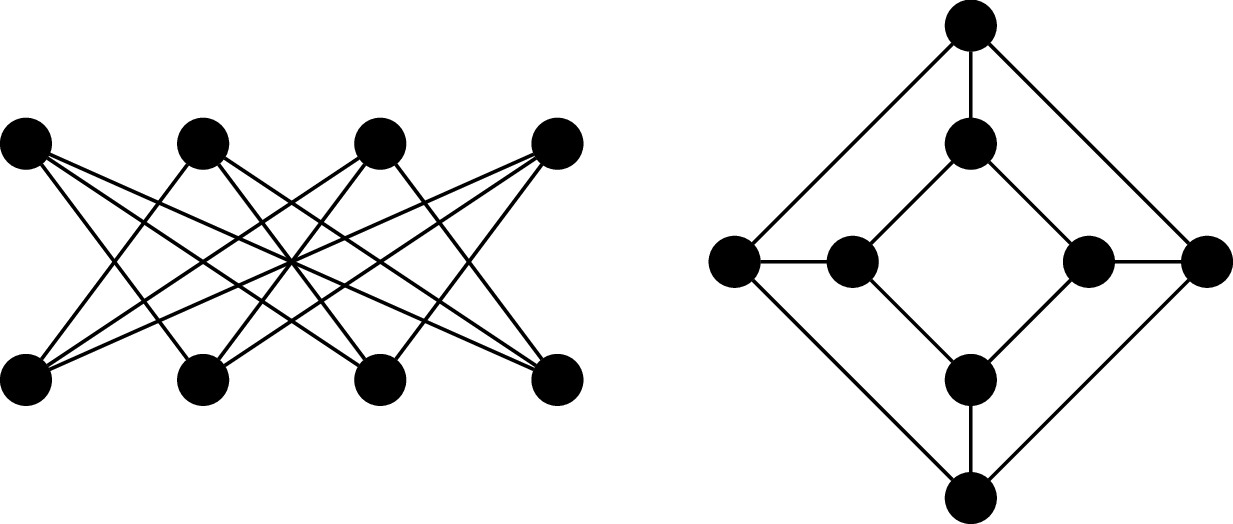
From the perspective of many applications, these graphs represented by these diagrams would be considered the "same". In fact, these are both diagrams of the hypercube $Q_3$

Although the visual representation of the graph is very convenient, it is sometimes misleading, because we're limited to 2D drawings. In fact, there is a vast area of research devoted to graph drawing and the mathematics of embedding graphs in two dimensions. The point of this is that two graphs may look very different, but turn out to be the same.

But even more fundamental than that, we intuitively understand that just because the graph isn't exactly the same (i.e., the vertices are named something differently) doesn't mean that we don't want to consider them equivalent. The next definition is how we define whether two graphs are basically the same, just with different names or drawings.

An isomorphism between two graphs $G_1 = (V_1,E_1)$ and $G_2 = (V_2,E_2)$ is a bijection $f:V_1 \to V_2$ which preserves adjacency. That is, for all vertices $u,v \in V_1$, $u$ and $v$ are adjacent in $G_1$ if and only if $f(u)$ and $f(v)$ are adjacent in $G_2$. Two graphs $G_1$ and $G_2$ are isomorphic if there exists an isomorphism between them. When $G_1$ and $G_2$ are isomorphic, we denote this by $G_1 \cong G_2$.

In other words, we consider two graphs to be the "same" or equivalent if we can map every vertex to the other graph such that the adjacency relationship is preserved. In practice, this amounts to a "renaming" of the vertices, which is what we typically mean when we say that two objects are isomorphic. Of course, this really means that the edges are preserved.

Consider the following graphs $G_1 = (V_1, E_1)$ and $G_2 = (V_2, E_2)$.

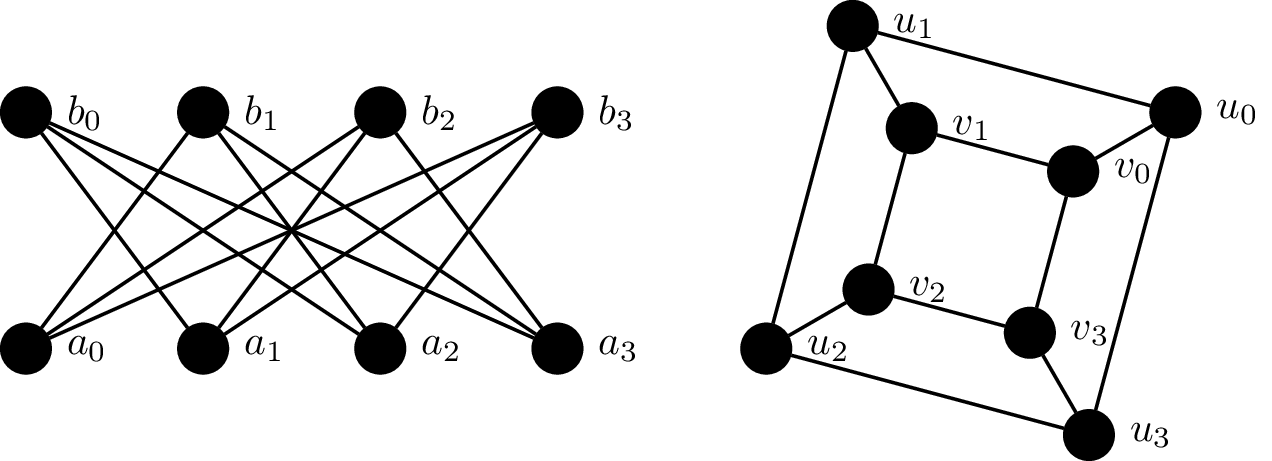
We will show that these two graphs are isomorphic by defining a bijective function $f:V_1 \to V_2$ which preserves adjacency: \begin{align*} f(a_0) &= u_0 & f(a_1) &= v_3 & f(a_2) &= u_2 & f(a_3) &= v_1 \\ f(b_0) &= v_2 & f(b_1) &= u_1 & f(b_2) &= v_0 & f(b_3) &= u_3 \\ \end{align*} This is a bijection, since every vertex in $V_1$ is paired with a vertex in $V_2$. We then verify that this bijection preserves adjacency by checking each edge under the bijection: \begin{align*} (f(a_0),f(b_1)) &= (u_0,u_1) & (f(a_0),f(b_2)) &= (u_0,v_0) & (f(a_0),f(b_3)) &= (u_0,u_3) \\ (f(a_1),f(b_0)) &= (v_3,v_2) & (f(a_1),f(b_2)) &= (v_3,v_0) & (f(a_1),f(b_3)) &= (v_3,u_3) \\ (f(a_2),f(b_0)) &= (u_2,v_2) & (f(a_2),f(b_1)) &= (u_2,u_1) & (f(a_2),f(b_3)) &= (u_2,u_3) \\ (f(a_3),f(b_0)) &= (v_1,v_2) & (f(a_3),f(b_1)) &= (v_1,u_1) & (f(a_3),f(b_2)) &= (v_1,v_0) \end{align*}

Determining if graphs are isomorphic

So an obvious and fundamental problem that arises from this definition is: Given two graphs $G_1$ and $G_2$, are they isomorphic? The obvious answer is that we just need to come up with an isomorphism or show that one doesn't exist. Unfortunately, to do this on a computer, there are $n!$ possible such mappings we would need to check. In fact, characterizing the complexity of solving the graph isomorphism problem is one of the most challenging problems in theoretical computer science. The most significant progress on this problem was made in 2015 (and 2017) by our own Lazlo Babai, who proved that graph isomorphism can be solved in $2^{O(\log^c n)}$ time for some constant $c$.

When determining if two specific graphs are isomorphic by hand, however, you can be clever and take shortcuts. A common tool is isomorphism invariants.

For example, $P(G) = |V|$ is clearly an isomorphism invariant, since the existence of a bijection implies the vertex sets have the same size. We can also show that $P(G)=|E|$ is an isomorphism invariant (exercise; one simple approach uses the handshaking lemma).

Assume $G_1\cong G_2$. We must show that $G_1$ and $G_2$ have the same degree sequence. Let $v_1,\ldots,v_n$ be the vertices of $G_1$ sorted by their degree; Then $(\deg(v_1),\ldots,\deg(v_n))$ is the degree sequence of $G_1$.

Since $G_1\cong G_2$, there exists a bijection $f$ between their vertex sets that preserves adjacency. Since $f$ is a bijection, the list $(\deg(f(v_1)), \ldots, \deg(f(v_n)))$ is also a list of the degrees of vertices in $G_2$.

Since $f$ preserves adjacency, for every $v_i$ in $G_1$, $\deg(v_i) = \deg(f(v_i))$. This means $$(\deg(f(v_1)), \ldots, \deg(f(v_n))) = (\deg(v_1),\ldots,\deg(v_n)).$$ Thus $(\deg(f(v_1)), \ldots, \deg(f(v_n)))$ is sorted as well, and is thus the degree sequence of $G_2$ as well as $G_1$.

Flipping around the definition of isomorphism invariant gives the following very simple theorem.

Here is an example of how this can be used. Consider these graphs:

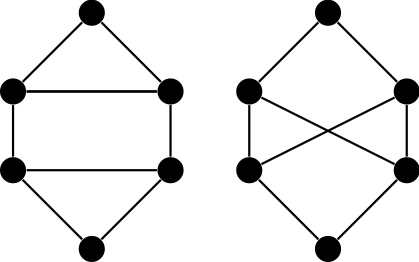
These graphs have the same degree sequence $(3,3,3,3,2,2)$, but they are not isomorphic; Theorem 10.21 does not apply! Here is one that works: Let $T(G)$ be the number of "triangles" in $G$ (that is, sets of three vertices that are all pairwise connected; we could say these are "copies of $K_3$".) This is an isomorphism invariant (exercise), and $T(G_1) = 2$ while $T(G_2)=0$.

Graph Coloring

A $k$-coloring of a graph $G=(V,E)$ is a function $c:V \to \{1,2,\ldots,k\}$ such that for all $uv\in E$, $c(u) \neq c(v)$. A graph is $k$-colorable if there a $k$-coloring of $G$. For a non-empty graph $G$, we define $\chi(G)$, called the chromatic number of $G$, to be smallest $k$ such that $G$ is $k$-colorable.

For any non-empty graph we have $\chi(G) \leq |V|$. An easy way to see why is to consider the following coloring for a graph of $n$ vertices: just color each vertex its own color.

We will use $k$-colorability as an invariant to show that two graphs are not isomorphic.

Consider the following two graphs, $G_1$ and $G_2$.

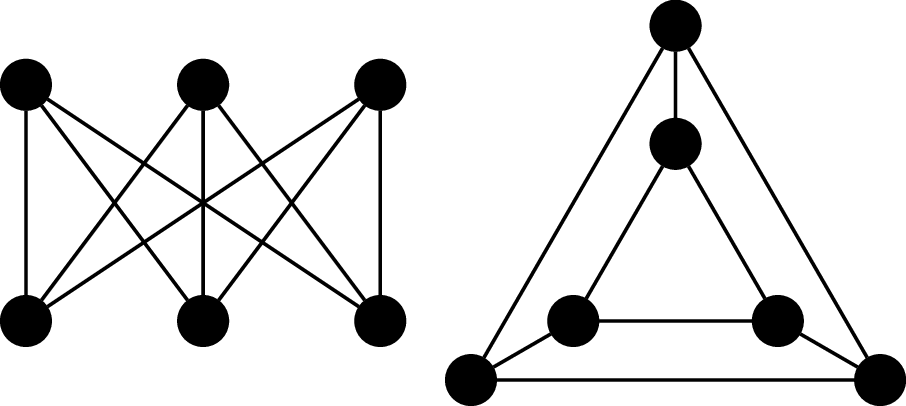
First, we observe that both graphs have 6 vertices and 9 edges and both graphs are 3-regular. However, we will show that $G_1$ is 2-colorable and $G_2$ is not. To see that $G_1$ is 2-colorable, we observe that the vertices along the top row can be assigned the same color because they are not adjacent to each other. Similarly, the vertices along the bottom can be assigned a second color.

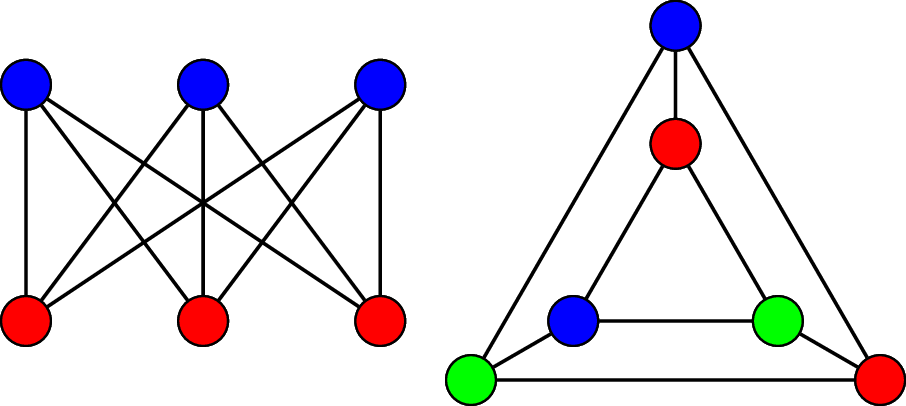
However, $G_2$ contains two triangles and by definition, the vertices belonging to the same triangle must be colored with 3 different colors. Since $G_2$ is not 2-colorable, the adjacency relationship among the vertices is not preserved.

CMSC 27100 — Lecture 10b

The notes for this course began from a series originally written by Tim Ng, with extensions by David Cash and Robert Rand. I have modified them to follow our course.

Proofs on Graphs

Graph Isomorphisms

Determining if graphs are isomorphic

Graph Coloring